2枚の鏡を直角に向き合わせ、その間に立ちます。
鏡が2枚なので、自分の姿は2個うつるかというと、そうではなく・・・

3つの像が見えます。

次に、鏡の角度を60度にしてみます。
すると像はさらに増え、5個になりました。

鏡の角度 像の数
90度 3
60度 5
30度 ???
では鏡の角度を 30度にすると、像はいくつできるでしょうか。
子供達はすぐにひらめきます。
「これは知ってる!規則性の問題だ!3、5の次は7だ。」
ほとんどの子はその答えます。しかし実際に調べてみると・・・

あれ、あれれ・・・?
もっといっぱいいます。数えてみると1、2、3・・・7、8・・・11。
鏡の角度 像の数
90度 3
60度 5
30度 11
なぜ像は11個もできてしまったのでしょうか。
2枚の鏡が90度で向き合っている場合の像を真上からみたのが下図です。
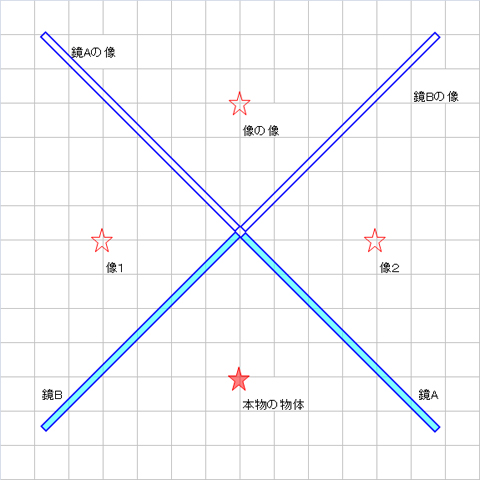
色が塗られているのが本物、白抜きになっているのが像です。
鏡A・Bにに直接うつる像は2つあり(像1・像2)、さらに鏡の像が2枚できてそれらによって像の像がつくられます。合計すると像は3つになります。
別に見方もできます。
上の図で、鏡と鏡にはさまれた空間は合計4個できています。
空間の角度が90度なので、それ以上はできません。(90×4=360度が最大)
さらにそれぞれの空間には像は1つずつあるので、物体は合計4つ見えるます。このうち1個が本物で、残り3個が像です。
つまり、像の数というのは部屋の数(360÷90)から本物の1個分を引いた数となり、「像の数=(360÷90)−1」という公式が導き出せます。
多くの受験生はこの公式を覚えます。そして「像の数の問題」が出たら「ははん、あの公式だったな」と、機械的に代入し、素早く答えを出します。
公式ができるということはその原理を頻繁に使うということでもあり、それを覚えた方が楽です。
しかし公式に頼っていると、物事の本質を見失ってしまうかもしれません。
今回、「合わせ鏡の公式」を覚えるのはやはり必要でしょうが、覚えて満足ではなく、本来それがどのような原理で生み出されたのか、それを自分で説明できるようになっておくと、応用が効いて数学や物理に強くなっていくような気がします。
4年生「鏡と光」より
|

